그래프 구조를 이용해 문제를 해결하기 위해
필요한 기본적이고 대표적인 그래프 알고리즘에서
BFS,DFS를 빼놓고 논하기는 쉽지 않을 것이다.
일단, 그래프 알고리즘을 말하기 전에 그래프에 대해서 말해보자.
그래프란?
그래프는 정점의 집합과 정점들을 서로 잇는 에지의 집합으로 구성된다.
수학적으로 표현하면 그래프 G = < V, E > 형태로 표현하고,
여기서 V는 정점의 집합, E는 에지의 집합을 나타낸다.
그래프에는 크게
방향 그래프, 무방향 그래프, 가중 그래프, 비가중 그래프가 있다.
만약 에지가 특정 정점에서 다른 정점으로 향하는 방향있다면 방향 그래프라고 한다.
특정 방향을 가리키지 않으면 무방향 그래프라고 한다.
에지에 가중치가 있으면 가중 그래프,
가중치가 없으면 비가중 그래프라고 한다.
(추가적으로 그래프를 다룰 때 노드와 정점은 같은 의미로 사용된다.)
이처럼 그래프는 매우 유연한 자료 구조입니다.
트리나 연결 리스트와 같은 다른 연결된 자료 구조는 그래프의 특별한 형태라고 볼 수 있습니다.
그래프는 객체(정점)와 객체 사이의 관계 (에지)를 표현할 수 있어서 유용합니다.
그래프에서 두 정점 사이에는 여러 개의 에지가 있을 수도 있고,
또한 하나의 에지에 여러 개의 가중치를 부여할 수도 있습니다.
특정 정점에서 나온 에지가 자기 자신으로 연결되는 셀프 에지도 만들 수 있습니다.
그래프는 다양한 에지와 정점의 표현을 가질 수 있습니다.
그래프의 일종인 하이퍼그래프는 여러 정점을 동시에 연결하는 에지를 가질 수 있고,
또 다른 변종인 혼합 그래프는 하나의 그래프 안에
방향 에지와 무방향 에지를 함께 가질 수 있습니다.
그래프는 범용적인 특징을 가지고 있어서 많은 응용 프로그램에서 사용되고 있습니다.
이론 컴퓨터 과학자들은 유한 상태 기계 또는 오토마타를 모델링하기 위해 그래프를 사용하고,
인공지능 및 머신 러닝 전문가들은 시간에 따른
네트워크 구조 변화로부터 정보를 추출하기 위해 그래프를 이용합니다.
방향 가중 그래프를 사용하는 알고리즘
이번 게시글에서는 주로 방향 가중 그래프를 사용하는 알고리즘에 대해 살펴볼 것이며,
경우에 따라 에지 가중치가 양수인 그래프만 다룰 것입니다.
이제,
너비 우선 탐색과 깊이 우선 탐색이라는
두 가지 주요한 그래프 탐색에 대해서 알아봅시다.
그래프 순회 문제
얼마 전에 새로운 동네로 이사했다고 가정해보자.
새로운 동네에서 새로운 이웃을 만다나 보니 사람드링 주변에 괜찮은 맛집을 추천해주었다.
여기서 추천받은 식당에 모두 방문해보고 싶어서 동네 지도를 꺼내
우리집과 식당을 지도에 표시했다.
지도에는 이미 이용할 수 있는 도로가 표시되어 있다.
우리집과 식당을 그래프의 정점으로 표현하고,
연결된 도로를 에지로 표현한 후, 우리 집에서 시작하여 모든 식당에 방문하려고 한다.
이처럼 그래프의 특정 정점에서 시작하여
나머지 모든 정점을 방문하는 문제를 그래프 순회 문제라고 한다.
아래 그림에서 정점 옆에 빨간색으로 쓰인 숫자는 정점의 ID이다.
1번 정점은 우리집을 나타내고, R1부터 R7까지의 정점은 식당을 나타낸다.
모든 길은 어느 방향으로든 이동할 수 있으므로,
에지에 화살표가 없는 무방향 에지로 표현했다.
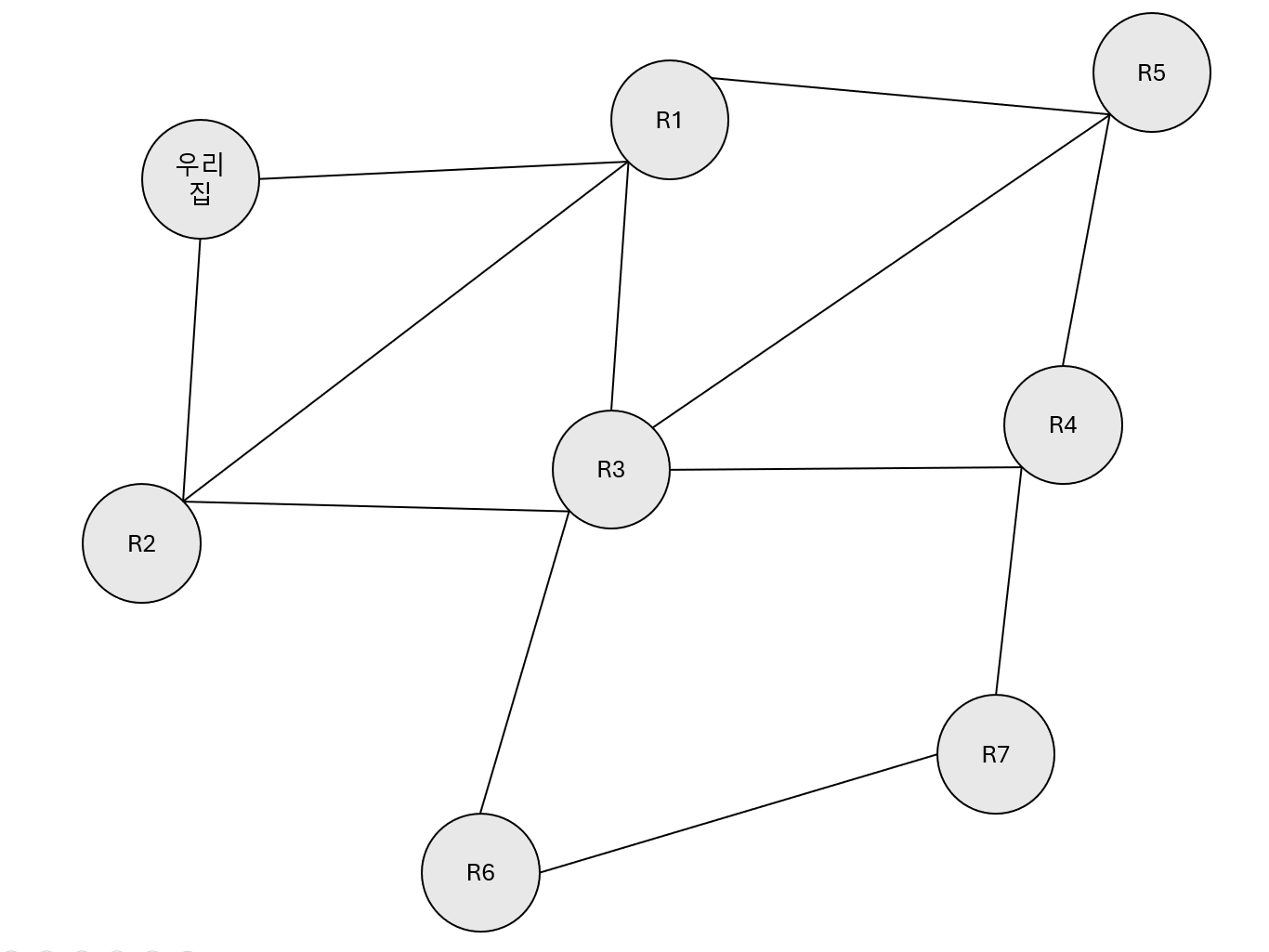
그래프 순회 문제를 수학적으로 표현하면
G = <V, E>가 주어질 때 특정 정점 s로부터 시작하여
모든 정점 v ∈ V를 방문하는 문제라고 할 수 있다.
그래프 순회 문제는 그래프에서 특정 정점을 찾기 위한 용도로 사용될 수 있기 때문에
그래프 탐색 문제라고 부른다.
여러 그래프 탐색 알고리즘이 존재하고,
각각은 서로 다른 순서로 모든 정점을 방문한다.
너비 우선 탐색
그래프에서 너비 우선 탐색은 시작 정점을 경계에 추가하는 것으로 시작한다.
경계는 이전에 방문했던 정점들에 의해 구성된다.
그리고 현재 경계에 인접한 정점을 반복적으로 탐색한다.
다음에 나오는 그림을 보면서 BFS 동작에 대해 자세히 알아보겠다.
1. 먼저 시작점인 '우리집' 정점을 방문한다.

2. R1과 R2를 방문한 후의 BFS의 상태이다.
R1과 R2는 어느 것을 먼저 방문해도 상관없다.
즉, 시작 정점과 같은 거리에 있는 정점들의 방문 순서는 임의로 정해도 된다.
시작 정점에서 멀리 있는 정점보다 가까운 정점을 먼저 방문해야 한다는 점이 중요하다.

3. 다음 그림은 R3와 R5, 그리고 R4와 R6 정점을 방문한 후의 BFS 상태이며,
전체 그래프를 순회하기 직전의 모습이다.

이처럼 BFS는 "가까운 것 부터 하나씩 탐색하는 과정"이다.
마치 나무의 가지를 한 층씩 넓게 탐험하는 것과 같다.
주로 자료구조 큐를 사용해서 구현하며, 최단 거리를 탐색하는 데 유리하다.
시작점에서 가까운 (이웃) 노드를 먼저 탐색한다.
이후 한 단계씩 이를 확장해나간다.
비유를 하자면 나무 밑둥에 서서 가장 가까운 가지부터 차례로 탐색하는 모습과도 같다.
BFS 구현하기
#include <string>
#include <vector>
#include <iostream>
#include <set>
#include <map>
#include <queue>
using namespace std;
template <typename T>
struct Edge
{
unsigned src;
unsigned dst;
T weight;
};
template <typename T>
class Graph
{
public :
// N 개의 정점으로 구성된 그래프
Graph(unsigned N) : V(N) {}
// 그래프의 정점 개수 반환
auto vertices() const { return V; }
// 전체 에지 리스트 반환
auto& edges() const { return edge_list; }
// 정점 v에서 나가는 모든 에지를 반환
auto edges(unsigned v) const {
vector<Edge<T>> edges_from_v;
for (auto& e : edge_list) {
if (e.src == v) {
edges_from_v.emplace_back(e);
}
}
return edges_from_v;
}
void add_edge(Edge<T>&& e) {
// 에지 양 끝 정점 ID가 유효한지 검사
if (e.src >= 1 && e.src <= V && e.dst >= 1 && e.dst <= V) {
edge_list.emplace_back(e);
}
else {
cerr << "에러 : 유효 범위를 벗어난 정점! " << endl;
}
}
// 표준 출력 스트림 지원
template <typename U>
friend ostream& operator << (ostream& os, const Graph<U>& G);
private:
unsigned V; // 정점의 개수
vector<Edge<T>> edge_list;
};
template <typename U>
ostream& operator << (ostream& os, const Graph<U>& G) {
for (unsigned i = 1; i < G.vertices(); i++) {
os << i << ":\t";
auto edges = G.edges(i);
for (auto& e : edges)
os << "{" << e.dst << ": " << e.weight << "}, ";
os << endl;
}
return os;
}
template <typename T>
auto create_reference_graph()
{
Graph<T> G(9);
map<unsigned, vector<pair<unsigned, T>>> edge_map;
edge_map[1] = { {2,0}, {5,0} };
edge_map[2] = { {1,0},{5,0},{4,0} };
edge_map[3] = { {4,0},{7,0} };
edge_map[4] = { {2,0},{3,0},{5,0},{6,0},{8,0} };
edge_map[5] = { {1,0},{2,0},{4,0},{8,0} };
edge_map[6] = { {4,0},{7,0},{8,0} };
edge_map[7] = { {3,0},{6,0} };
edge_map[8] = { {4,0},{5,0},{6,0} };
for (auto& i : edge_map) {
for (auto& j : i.second) {
G.add_edge(Edge<T>{i.first, j.first, j.second});
}
}
return G;
}
template <typename T>
auto breadth_first_search(const Graph<T>& G, unsigned start)
{
queue<unsigned> queue;
set<unsigned> visited; // 방문한 정점
vector<unsigned> visit_order; // 방문 순서
queue.push(start);
while (!queue.empty())
{
auto current_vertex = queue.front();
queue.pop();
// 현재 정점을 이전에 방문하지 않았다면
if (visited.find(current_vertex) == visited.end())
{
visited.insert(current_vertex);
visit_order.push_back(current_vertex);
for (auto& e : G.edges(current_vertex))
{
// 인접한 정점 중에서 방문하지 않은 정점이 있다면 큐에 추가
if (visited.find(e.dst) == visited.end())
{
queue.push(e.dst);
}
}
}
}
return visit_order;
}
int main()
{
using T = unsigned;
// 그래프 객체 생성
auto G = create_reference_graph<T>();
cout << "[입력 그래프]" << endl;
cout << G << endl;
// 1번 정점부터 BFS 실행 & 방문 순서 출력
cout << "[BFS 방문 순서]" << endl;
auto bfs_visit_order = breadth_first_search(G, 1);
for (auto v : bfs_visit_order)
cout << v << endl;
}
'컴퓨터 프로그래밍 공부 > 자료구조와 알고리즘' 카테고리의 다른 글
| DFS 구현 (재귀와 스택) 과 BFS(큐) (2) | 2024.12.27 |
|---|---|
| 윈도우 인스톨러 (2) | 2024.12.17 |
| 자기 전 누워서 정리하는 배열과 리스트 (0) | 2024.11.27 |
| 힙을 이용한 데이터 리스트 병합 (0) | 2024.11.18 |
| 힙을 이용한 중앙값 구하기 (0) | 2024.11.04 |