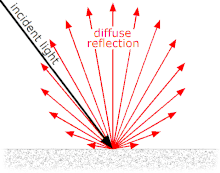
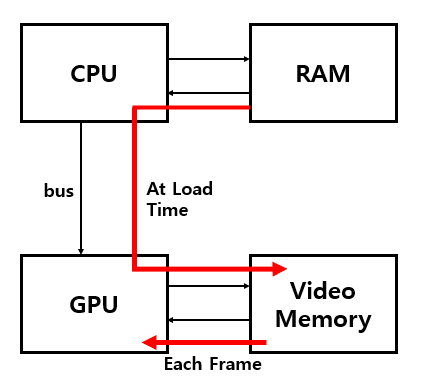
CPU에서 GPU로 데이터를 전송할 때는 비교적 속도가 느리니,최대한 단순하게 계산해서 접근할 수 있도록 하는 것이 좋다. 이러한 이론을 실제 코드로 구현하는 방법은여러 개의 변환을 순서만 잘 정리하면 하나의 변환 행렬로 만들 수 있다.따라서 결과적으로 GPU에게 회전과 이동을 한 하나의 변환 행렬만 보내면 된다. 이러한 변환에는Model Matrix, View Matrix, Projection Matrix가 같이 사용된다.위 3 가지는 나중에 추후 따로 더 자세하게 정리해보겠다. 이번 포스팅에서는 Model Matrix와 Invertranspose 두 가지를 사용해서쉐이더의 코드를 작성해볼 것이다. 노멀 벡터 노멀 벡터를 회전을 시킬 때는다른 방식을 사용해야 한다.물체를 회전을 시킨다면, 물체의 표면..