어떤 점을 원점에 대해서 회전시키는 경우
어떤 점을 원점에 대해서 회전시키는 경우에
어떠한 점 (= 임의의 점) xy를 하나의 미지수 (x,y)로 표현할 수 있고,
그 임의의 점을 원점(여기서 원점은(0,0)이 아닐 수도 있다.)을 기준으로
θ만큼 회전 시킨 지점을 (x',y')로 표현할 수 있다.

그러한 (x',y') 지점을 구하는 식은 아래와 같다.

그럼 열벡터(Column Vector) 형태의 회전 변환을
행벡터(Row Vector)형태의 회전 변환 할까?
방법은 간단하다.
좌변에도 전치(Transpose)를 해주고,
우변에도 전치(Transpose)를 해준다.
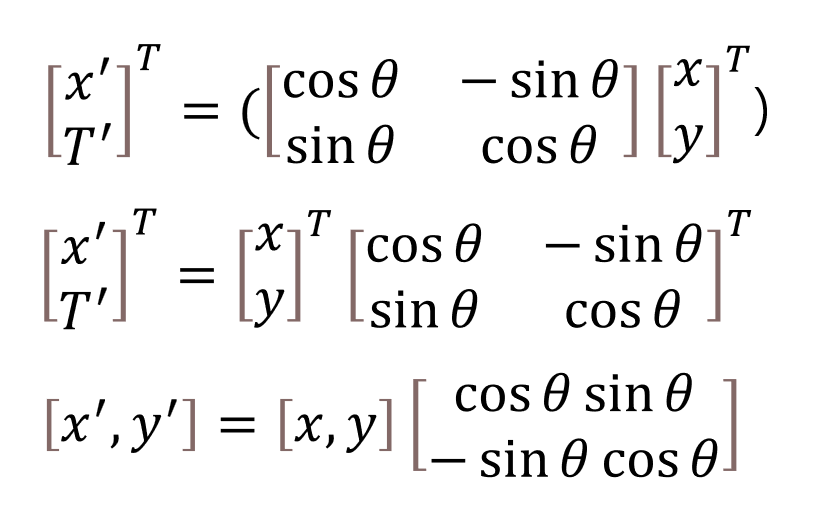
이 식의 전개를 글로 풀어보면 다음과 같다.
좌변에 Transpose를 해주고,
우변에도 통째로 Transpose를 해준다.
이 Column vector는, 결국에는 괄호로 감싸져있는 행렬의 곱이다.
행렬곱을 괄호로 감싼뒤 Transpose를 해주는 것은,
각각을 Transpose로 해주는 것으로 바꿀 수 있다.
여기서 주의해야할 점은 순서가 뒤바뀐다는 것이다.
이러한 연산을 끝내면 결국에는 row vector 형식의 Transpose로 바뀐다.
변환행렬을 전치해주기만 한다면,
결국에는 row vector든, colum vector인지는 중요하지 않다.
어떤 점을 이동 시키는 경우
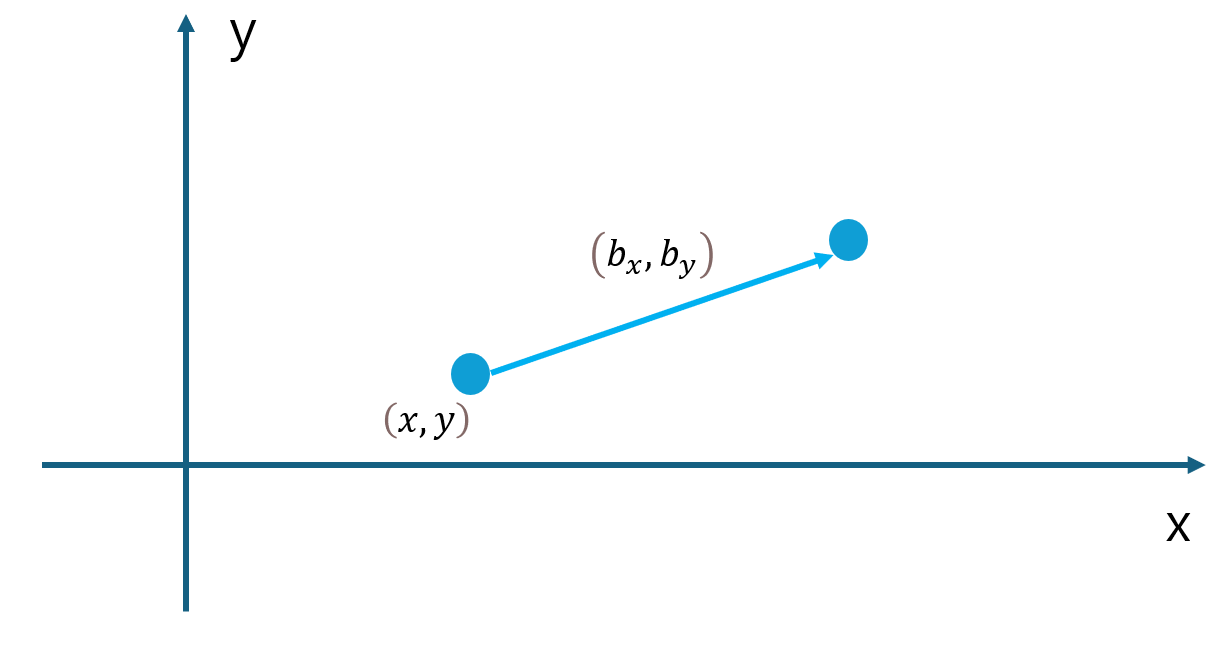
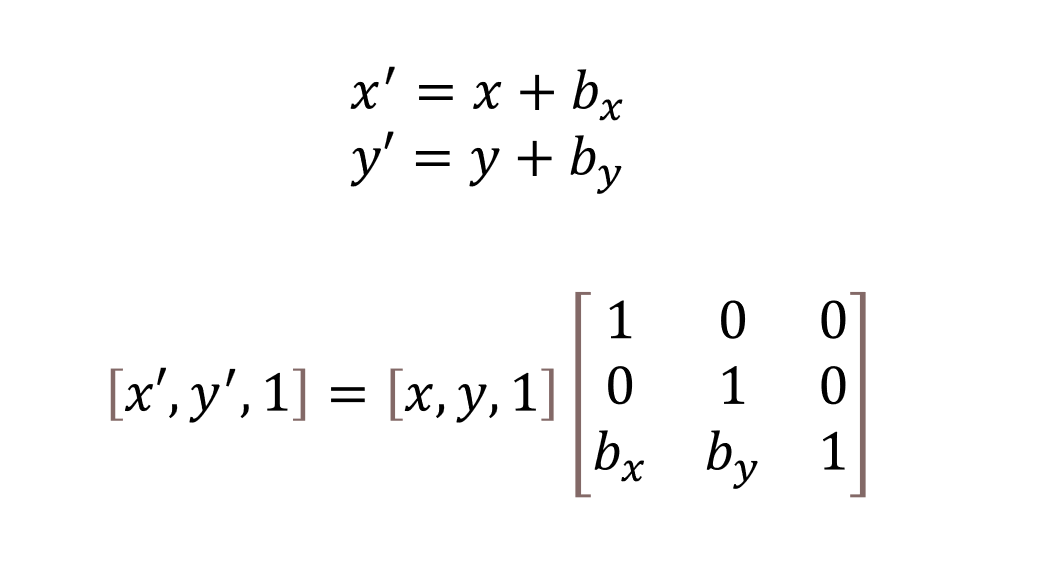
x' = x + bx
y' = y + by 라는 식을 행력식으로 표현하면
위에서 보이는 행렬과 같다.
벡터/포인트의 회전과 이동을
하나의 행렬로 표현하기
위 예시를 보면서
어 회전하고 이동을 각각 따로 두기보다 합치는 것도 가능하지 않을까?
싶으실 수 있다.
그럼
위의 전개한 식을 응용하여
회전과 이동을 동시에 하는 행렬은 어떻게 될까?

그 행렬은 다음과 같이 표현할 수 있다.
회전따로, 이동따로 하기보단 한번에 처리하는 것이
편리하시다 느끼신다면, 아래의 식을 이용해주시면 된다.

자, 우리가 쓰는 DX는 왼손좌표계를 쓴다.
또한 DX는 row-major로 다루고,
HLSL에서는 column-major로 다룬다.
따라서 전치로 전달하여 맞춰줘야 하기 때문에,
전치를 행렬로 표현함에 있어서 자유로워야 하며,
이러한 행렬 표현식을 코드로 표현하기 위해서는
위 과정을 꼭 숙지해야한다.
'그래픽스 > DX11' 카테고리의 다른 글
| D3D11 회전축에 대한 벡터의 회전 (1) | 2024.12.13 |
|---|---|
| D3D11 선형 변환(Linear Transformation) - 동차성과 가법성 (0) | 2024.12.12 |
| D3D11 Rasterization - Light (0) | 2024.10.30 |
| DX11 - 쉐이딩(Blinn-Phong Shading) (0) | 2024.10.25 |
| DX11 - 원근 투영(Perspective Projection) (0) | 2024.10.23 |