개발 공부 블로그

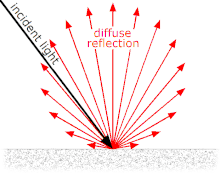
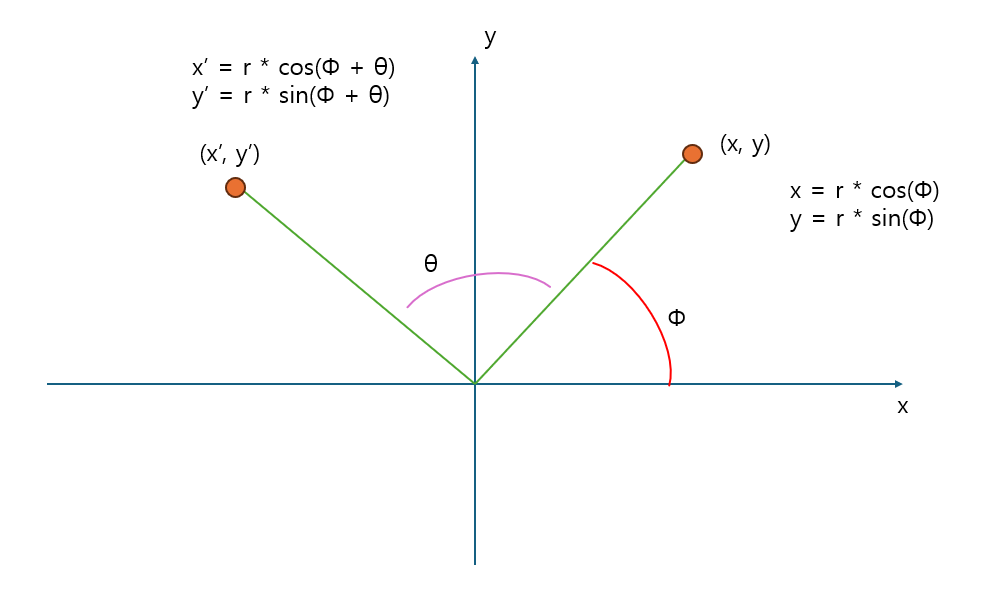
쉐이딩은 조명과 재질의 상호작용을 고려해서 색을 결정하는 과정이다. 이때 vs에서 미리 색을 결정해서 ps에서 보간하는 방법이 있고, 쉐이딩 알고리즘 자체를 ps에서 하는 방법이 있다. 둘 중에 어느 것이 다 빠르나면, 픽셀수에 비해 vertex의 수가 훨씬 적기 때문에 vs에서 돌리는 것이 더 빠르다. 대신에 렌더링의 상세도는 조금 떨어질 것이다. 요즘에는 GPU가 많이 빨라졌기 때문에 ps에서 돌리는 경우도 많다. 오늘은 ps에서 blinn-pong shading을 구현한다. 회전 회전을 할 때는 어떤 회전 축에 대해 회전할 것인지 정해야한다. DX는 왼손 좌표계를 사용하고 있기 때문에 Y축을 기준으로 회전시킨다면, 왼손을 엄지를 위로 쭉 펴고 나머지 손가락들을 감아주는 방향으로 회전하는 것과 같다...

원근 투영은 원근법에 대한 것으로,원근범에 대한 기본적인 방식은 먼 거리에 있는 물체가더 작게 보이게 2D 화면에 나타내는 방식이다.3D 투영 (또는 그래픽 투영)은 2차원 (2D) 표면에3차원 (3D) 객체를 표시하는 데 사용되는 디자인 기술이다. 원근법을 적용한 그림들의 공통점은 '소실점의 존재'이다.이 소실점을 기준으로 일정 각도만큼의 직선들을 나란히 그리게 되면실제로 소실점에 가까운 부분들은 멀어보이게 되는 시각적 효과를 가져온다. 하지만, 3D 컴퓨터 환경에서 원근법을 적용하기 위해선실제 그림에서 적용되는 방식과는 조금 다르다.결론은 3D Rendering 에서는 소실점 개념은 필요치 않다. 우선, 한가지 생각해볼 문제는 우리가 바라보는 위치즉, 3D 공간을 표현하기 위한 우리의 시계에서는'카메..

이번 강의에서는 렌더링 파이프라인의 각 화살표 단계에서 쉐이더가 무슨 일을 하는지, 왜 필요한지, 왜 이런 구조로 만들어 졌는지 알아보기 위해서 마치 쉐이더라는 것을 활용하는 것 처럼 짜본다. 쉐이더의 이름은 쉐이딩를 할 때 사용해서 쉐이더라는 이름이 붙기 시작했다. 입체감을 주기 위해서 음영처리를 하기 위해서 처리하는 단계이다. 가상 세계에서 정말로 3차원에 있는 것처럼 보이기 위해 빛과 물체의 표면의 상호작용을 고려해서 음영처리 하는 것을 시작으로 GPU안에서 작동하는 프로그램을 쉐이더라고 부르기 시작했다. 쉐이더에 공통적으로 들어가는 것은 스케일, 트랜스레이션, 로테이션 값이다. 같은 물체 안에 동일한 변환을 적용하는 것들은 따로 모아놓고 사용하셨다. 버텍스 쉐이더에서 가장 중요한 것은 어떠한 정보..

렌더를 할 때, CPU가 처리할 기하 정보와 GPU가 처리할 버퍼 정보는 서로 다르다. 정점의 정보와 정점과의 연결관계, 그리고 컬러의 값은 기하 정보이며, 그 정보 값을 토대로 처리할 버퍼를 따로 변수로 둬야한다. 이후 버퍼와 값을 한 함수에 묶어줘서 컴퓨터에게 넘겨주면 컴퓨터가 이를 처리하는 것으로 알고 있었는데, 홍랩에서는 버퍼로 현재 값을 복사하고 있었다. 실제로 DX를 사용하면 cpu에 있는 것을 gpu에 복사하고, 다시 그 값이 변경되고 그 다음에 렌더링이 생기는 과정을 거치는 것을 해당 수업을 통해서 알았다. 오늘날의 GPU CPU 값 전달 방식은, GPU가 데이터를 VRAM에 저장한 상태에서 CPU에서 그렇게하는 신호가 오면 VRAM에서 데이터를 가져와 연산하는 방식이다. 이는 그래픽 카드..

일반적으로 우리가 머리 속으로 생각하는 형상을 그래픽으로 표현한 것을 모델이라고 한다. 이러한 것을 3차원으로 표현하기 위해 우리는 메쉬라는 작은 삼각형을 이용해서 모델을 만든다. 그렇다면 이번에는 뭘 만드는 것이 중점이냐면, 2차원 환경에서 삼각형으로 이루어진 물체를 시계 방향과 반시계 방향으로 회전시키고 비율을 줄여보고 늘려볼 수 있다. 또한 중점을 중심으로 회전하는 것과 자기 자신을 회전하는 것 등 이동과 관련에 대한 실습을 해보는 것이 해당 강의의 목표이다. 1. 모델의 이동 모델을 이동시키기 위해서는 각 정점의 현 위치에서 이동시키고자 하는 거리까지 더해주면 된다. 2. 모델의 회전 2차원 회전에서는 어떤 점에 대해서 회전하는 지가 중요하고 3차원 회전에서는 어떤 축에 대해서 회전하는 지가 중요..

원은 여러 개의 삼각형을 쪼개어 만든다. 얘를 들어 삼각형을 그린다고 했을 땐, 삼각형0은 vertex 0 2 1 삼각형1은 vertex 0 3 2 ... 이런 식으로 사용할 것이다. 이럴 때 vertex의 순서가 중요하다. 해당 엔진에서는 Vertex 순서가 시계 방향으로 가면 화면에 그려지지만, 반시계 방향으로 그린다면 화면에 제대로 그려지지 않는다. 이러한 방향은 사실 원하는 대로 바꿀 수 있다. 하지만, dx에서는 전통적으로 시계 방향으로 렌더하는 것이 앞면이라고 여긴다. 이러한 삼각형을 원처럼 보이도록 여러개를 쪼개어, sin과 cos을 이용하여 애둘러쌓아 둔다면 원처럼 보인다. 이러한 방식으로 원을 그리면 모든 삼각형이 0번을 공유한다. 하지만 마지막 삼각형은 1번 정점으로 다시 돌아오기 때문..

lighting은 물체와 빛 사이의 상호작용을 말한다. 사실적인 그래픽을 위해서 lighting이 매우 중요하다. 이러한 linghting 기법 중 하나인 퐁라이팅은 빛을 반사하는 것을 ambient, diffuse, specular, emissive 4가지로 나누어서 표현한다.diffuse는 난반사를 의미하며, 광원으로부터, 광원으로부터 점P까지의 벡터를 l, (normal vector 법선 벡터는 해당 직선이나 평면에서 수직인 벡터를 말한다) 점 P의 normal을 n으로 표현한다. 두 벡터 사이의 각이 작으면 작을수록 점 P는 더 많은 조명을 받게 될 것이다. 점 P로 들어오는 빛의 양은 두 벡터의 내적 값이라고 정의할 수 있다. 즉, 조명의 위치에 따라서 표면이 얼마나 밝아질 지를 정할 수 있다...

Interpolation v1에서 v2까지의 거리가 있다고 가정했을 때. v0은 v1,v2 중간 어딘가에 있다, 이때, v1에서 v0까지 거리를 a라고 할 때, v0에서 v2는 b이다. 그럼 v0이 v1에 가까워지면 b가 커지고, v0이 v2에 가까워지면 a가 커지는 것을 알 수 있다. 이러한 v는 다음과 같이 표현할 수 있다. v = b/a+b* v1 + a/a+b *v2 여기서 b/a+bv1을 w라고 표현하면, a/a+b * v2는 1-w로 표현할 수 있다. 그럼 이제… 세 점 사이의 정 가운데 p가 있다고 해보자. 세 점은 각각 v1, v2, v3라 할 때 p를 다음과 같이 표현할 수 있다. p = v1 + v2 + v3 / 3 = 1/3 v1 + 1/3 v2 + 1/3 v3 = w1v1 + w2v..

벡터 동차 계산 보통 1이면 포인터이다(0이 아니면 포인터), 0이면 벡터이다. 가장 마지막이 동차좌표계이다. 레스터화가 빠른 이유 레스터화가 빠른 이유를 설명하기 전에, 비교군인 레이트레이싱을 설명하겠습니다. 레이트레이싱 우리가 가장 많이 사용하는 알고리즘은 레이트레이싱 (역방향 알고리듬) 이다. 이 알고리듬은 시점에서 ray를 쏘고, 이 ray가 hit하게되면, 색을 결정한 다음에 hit point의 픽셀을 계산하여 렌더링하는 기술이다. 근데 모든 픽셀을 계산하려면 모든 픽셀에 광선을 쏘개된다. 만약 픽셀이 10만개면 최소 광선을 10만개는 쏴줘야한다. 레이트레이싱에서 가장 부담이 되는 것은 광선하고 물체가 충돌하는 부분을 계산해야 된다는 것입니다. 이러한 이론적인 것을 코드화하면 레이트레이싱은 다음..

구의 Reflection 수치 값을 변경해주기 전이다. 구 1개만 반사 적용 구 2개에 반사광 적용 바닥까지 반사광 적용 이는 레이트레이싱을 이용한 반사광 적용이다. 반사되는 횟수가 많아질수록 고성능을 요구하기 때문에 컴퓨터 사양에 따라 좀 느려지기도 한다. 해당 이론은 Bilinear Interpolation즉 이중선형 보간과 관련이 있다. 우리는 해당 그림을 통해서 먼저 두개의 선형 보간을 수행하여 a와 b를 계산한 다음 a와 b를 보간하여 c를 찾을 수 있다. c는 당연히 (tx , ty)의 값을 가지게 될 것이다. 이중선형 보간은 일반 2D 그리드의 임의 위치에 있는 값을 알아야 할 때 사용된다. 이 그리디는 이미지나 텍스처 맵에 사용될 수 있다. 이 예에서는 녹색 점으로 표시된 위치(좌표 cx,..