앞선 게시글에서 해시 테이블을 이용하여 필요한 키를 저장하고 검색하는 방법에 대해 알아보았다.
그러나 다수의 키가 같은 해시 값을 갖는 충돌 문제가 발생한다는 점도 배웠다.
이전 예시에서는 같은 해시 값을 갖는 키에 대해서는
기존 키를 덮어써서 가장 최근에 추가된 키만 유지되도록 했었다.
그러나 이 방식은 다수의 키글 저장할 수 없는 문제가 있다.
그러므로 이러한 문제를 해결하고
해시 테이블에 모든 키를 저장할 수 잇는 몇 가지 방법에 대해 알아보자.
해시 테이블에서 충돌 해결 방법
1. 체이닝
2. 열린 주소 지정
2-1 .선형 탐색
2-2. 이차함수 탐색
3. 뻐구기 해싱
체이닝
앞에서는 하나의 해시 값에 대해 하나의 원소만을 저장했다.
그래서 특정 해시 값 위치에 이미 원소가 존재한다면
새로운 값과 예전 값 중 하나를 버릴 수 밖에 없었다.
체이닝(chaining)은 두 값을 모두 저장할 수 있는 여러 방법 중 하나이다.
이 방법은 해시 테이블의 특정 위치에서 하나의 키를 저장하는 것이 아니라
하나의 연결 리스트를 저장한다.
그러므로 새로 삽입된 키에 의해 충돌이 발생하면 리스트의 맨 뒤에 새로운 키를 추가한다.
따라서 다수의 원소를 원하는 만큼 저장할 수 있다.
벡터 대신 연결 리스트를 사용하는 이유는 특정 위치의 원소를 빠르게 삭제하기 위함이다.
열린 주소 지정
충돌을 해결하는 다른 방법으로 열린 주소 지정(open addressing)이 있다.
이 방법은 체이닝처럼 해시 테이블에 추가적인 리스트를 붙여서 데이터를 저장하는 방식이 아니라
모든 원소를 해시 테이블 내부에 저장하는 방식이다.
그러므로 해시 테이블의 크기가 반드시 데이터 개수보다 커야 한다.
열린 주소 지정 방법의 핵심은 특정 해시 값에 해당하는 위치가 이미 사용되고 있다면
테이블의 다른 비어 있는 위치를 탐색하는 것이다.
이떄 다른 비어 있는 위치를 찾는 방법은 여러 가지가 있을 수 있으며,
이제부터 여러 탐색 방법을 하나씩 알아보자.
선형 탐색
선형 탐색은(linear probing)은 가장 간단한 탐색 방법이다.
선형 탐색은 특정 해시 값에서 충돌이 발생하면 해당 위치에서
하나씩 다음 셀(cell) 위치로 이동하면서
셀이 비어 있는지를 확인하고, 비어 있는 셀을 찾으면 원소를 삽입한다.
즉, hash(x)에 해당하는 셀이 이미 채워져 있다면 hash(x + 1) 위치의 셀을 확인한다.
만약 hash(x + 1) 셀도 사용 중이라면 다시 hash(x + 2)셀을 검색한다.
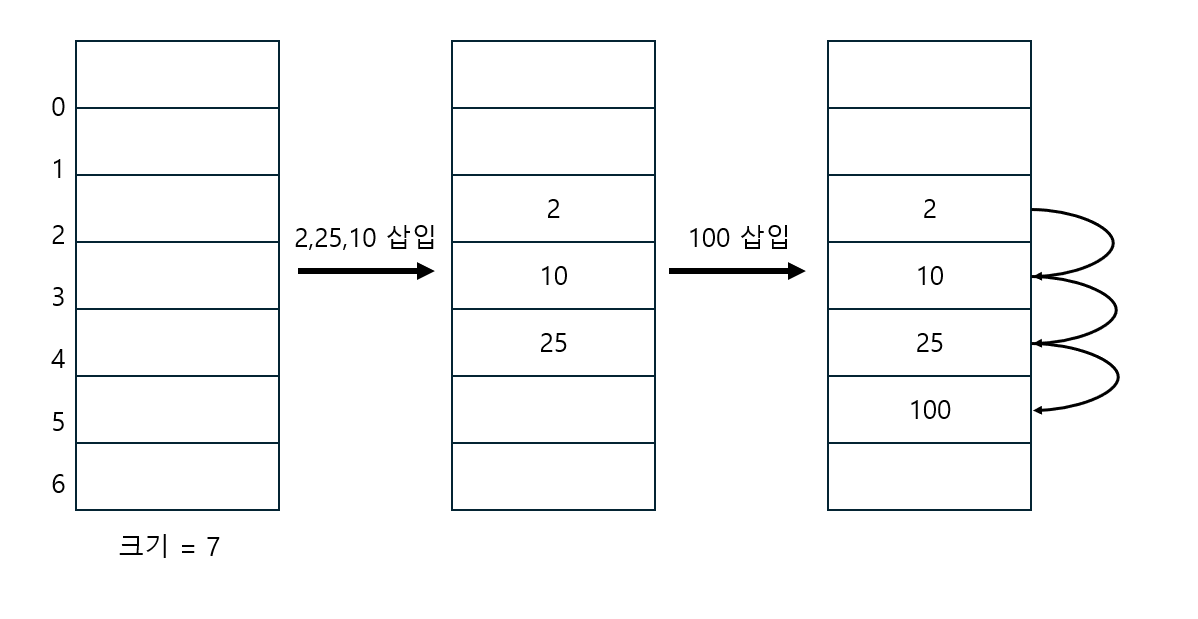


그림 3-7에 나타났듯이
주어진 데이터의 해시 값에 해당하는 위치가 이미 다른 값으로 채워져 있다면
다음으로 비어 있는 위치에 새 데이터를 삽입한다.
그림 3-7에서 처음에 세 개의 원소를 삽입했더니
해시 테이블의 특정 위치에 서로 인접한 군집 형태로 값이 채워졌다.
만약 이 구간에 해시 값을 갖는 새 원소가 들어오면 이 군집은 더욱 커지게 된다.
만약 원소 검색을 할 경우, 해시 함수에서 반환한 위치가 큰 군집의 시작 위치를 가리킨다면
클러스터의 맨 마지막 위치까지 선형 탐색을 해야 한다.
그러므로 검색 속도가 크게 느려질 수 있다.
즉, 데이터가 특정 위치에 군집화디는 경우에 문제가 발생하게 된다.
데이터가 군집화된다는 것은 해시 값이 너무 자주 발생해서
데이터가 몇 개의 그룹으로 뭉치는 형태로 저장된다는 의미이다.
예를 들어 크기가 100인 해시 테이블이 있는데,
대부분의 키가 3에서 7사이의 해시 값으로 변환된다고 생각해보겠다.
이 경우 대부분의 데이터가 3 ~ 7 이후 위치에 차례대로 저장될 것이고,
이로 인해 검색 속도는 급격하게 느려질 것이다.
이차함수 탐색
선현 탐색의 가장 큰 문제점은 군집화이다.
충돌이 발생하면 군집을 차례대로 검사해야 하기 때문이다.
이를 해결하기 위해 선형 방정식이 아닌 이차 방정식을 사용하여 탐색을 수행할 수 있다.
이러한 방식의 탐색을 이차함수 탐색(quadratie probing)이라고 한다.
예를 들어 데이터 x를 hash(x) 위치에 삽입하려고 한다.
만약 이 위치가 이미 사용 중이라면 hash(x+1^2)로 이동하고,
그 다음은 hash(x+2^2)으로 이동한다.
이처럼 이동 폭을 이차함수 형태로 증가시키면 데이터 군집이 나타날 확률은 상대적으로 줄어든다.
선형 탐색 및 이차함수 탐색은 모두 원소 위치가 기존에 삽입되어 있는
다른 원소들에 의해 영향을 받는다.
이때 기존에 저장되어 있던 원소는
새로 삽입하는 원소와 서로 다른 해시 값을 가질 수도 있다.
즉, 특정 해시 값을 갖는 키가 오직 하나만 존재한다 하더라도
충돌이 발생할 수 있다.
예를 들어 선형 탐색에서 해시 값이 4인 키가 두 개 있는 경우,
하나는 4위치에 삽입하고 다른 하나는 5위치에 삽입한다.
이후 해시 값이 5인 키를 새로 삽입해야 한다면 이는 6위치에 삽입해야 한다.
이 키는 다른 원소와 중복된 해시 값을 갖지 않았지만 저장되는 위치에는 영향을 받는다.
뻐구기 해싱
뻐꾸기 해싱(cuckoo hashing)은 완벽한 해싱 기법 중의 하나이다.
앞에서 언급했던 방법들은 최악의 상황에서는 O(1)의 시간 복잡도를 보장하지 않지만
뻐꾸기 해싱은 구현만 제대로 한다면 O(1)을 만족한다.
뻐꾸기 해싱은 크기가 같은 두 개의 해시 테이블을 사용하고,
각각의 해시 테이블은 서로 다른 해시 함수를 가진다.
모든 원소는 두 해시 테이블 중 하나에 있을 수 있으며,
그 위치는 해당 해시 테이블의 해시 함수에 의해 결정된다.
뻐꾸기 해싱이 이전에 설명한 해싱 기법과 다른 점은 다음과 같다.
- 원소가 두 해시 테이블 중 어디든 저장될 수 있다.
- 원소가 나중에 다른 위치로 이동할 수 있다.
앞서 언급한 해싱 방법에는 재해싱을 수행하지 않는 이상
원소가 최초 삽입된 위치에서 다른 위치로 이동할 수 없었다.
그러나 뻐구기 해싱 방법에서는 모든 원소가 두 개의 저장 가능한 위치를 가지며,
상황에 따라 이동할 수 있다.
더 나은 성능을 얻고 재해싱 빈도를 줄이기 위해 저장 가능한 위치 개수를 증가시킬 수도 있지만,
해당 게시글에서는 두 개의 해시 테이블을 사용하는 뻐꾸기 해싱 방법에 대해서만 알아보겠다.
룩업의 경우, 특정 원소가 존재하는지를 알기 위해 저장 가능한 위치 두 군데만 확인해보면 된다.
그러므로 룩업 연산의 시간 복잡도는 항상 O(1)이다.
그러나 삽입 연산은 좀 더 오래 걸리 수 있다.
A라는 원소를 삽입한다고 가정해보겠다.
삽입 함수는 먼저 첫 번째 해시 테이블에서 A를 삽입할 위치를 찾아 현재 비어 있는지를 검사한다.
만약 해당 위치가 비어 있다면 그대로 A를 삽입하면 된다.
그러나 해당 위치에 이미 다른 원소 B가 저장되어 있다면,
해당 위치에 A를 저장하고 B를 두 번쨰 해시 테이블로 옮긴다.
만약 B가 이동할 위치에 이미 다른 원소 C가 저장되어 있다면,
해당 위치에 B를 저장하고 C를 첫 번째 해시 테이블로 옮긴다.
이러한 작업을 완전히 비어 있는 셀이 나타날 때까지 재귀적으로 반복한다.
이러한 과정을 그림으로 나타내보겠다.
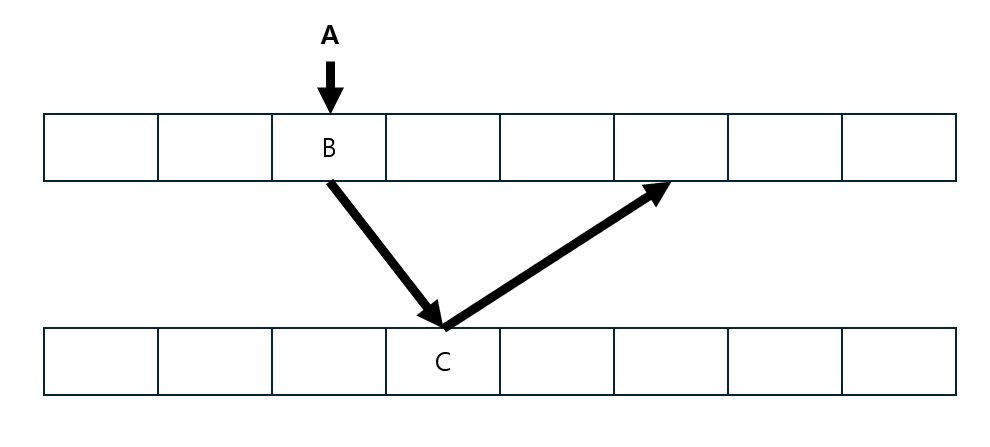
이러한 과정에서 만약 순환 (cycle)이 발생한다면 무한 루프에 빠질 수 있다.
예를 들어 위 그림에서 C가 옮겨가야 할 위치에 다른 원소 D가 있고,
D를 옮기다 보니 다시 A 위치를 방문한다고 가정하겠다.
이러한 경우가 순환이 발생하는 경우이며, 아래 그림을 참고 바란다.
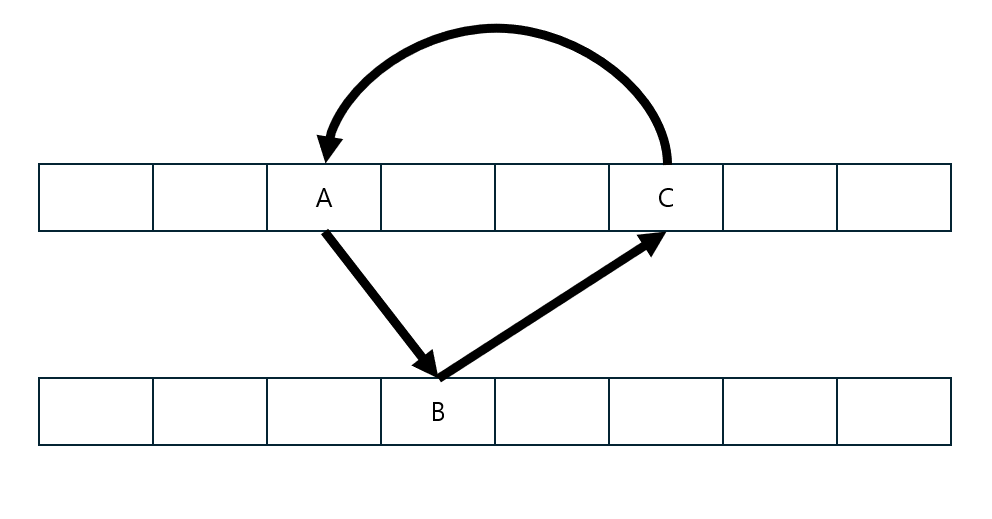
일단 순환이 발생했다면 새로운 해시 함수를 이용하여 재해싱을 수행해야 한다.
새로운 해시 함수를 사용하여 해시 테이블을 새로 구성한 경우에도
다시금 순환이 발생할 수 있으므로 여러 번 재해싱을 수행해야 할 수도 있다.
그러나 적절한 해시 함수를 사용하면
높은 확률로 O(1)의 성능을 갖는 해시 테이블을 구성할 수 있다.
열린 주소 지정 방법과 마찬가지로
뻐꾸기 해싱도 전체 해시 테이블 크기 이상의 원소를 저장할 수 없다.
높은 성능을 보장하려면 부하율이 0.5보다 작게끔 설정해야 한다.
즉, 전체 원소 개수가 해시 테이블 크기의 절반보다 작아야 한다.
C++ 해시 테이블
대부분의 응용 프로그램에서 룩업 연산은 매우 빈번하게 발생한다.
그러나 해시 구현에서 항상 양의 정수만 취급할 수는 없다.
오히려 문자열 데이터를 다루게 되는 경우가 더 많다. 다시 영어 사전을 예로 들어보겠다.
영어 사전을 구현하려면 영어 단어를 키로 사용하고, 단어 뜻을 값으로 사용해야 한다.
병원 기록 데이터베이스의 경우에도 환자 이름이 키가 되고,
환자와 관련된 정보는 값으로 취급해야 한다.
정수로부터 해시 값을 계산하기 위해 사용했던 모듈로 함수는 문자열에는 적용할 수 없다.
간단한 해결책은 문자열의 모든 문자에 대한
ASCII 코드 값을 모두 더한 후에 모듈로 연산을 하는 것이다.
그러나 같은 문자로 구성된 문자열이 너무 많아서 충돌이 빈번하게 발생할 수 있다.
C++는 문자열로부터
해시 값을 생성하는 용도로 std::hash<std::string>(std::string) 함수 객체를 제공한다.
이 함수 객체 내부에는 해시 함수 알고리즘이 구현되어 있다.
C++는 문자열 이외에도 모든 기본 데이터 타입에 대한 해시 값을 생성하는 기능도 제공한다.
/* 설명 추가하기 */
블룸 필터
블룸 필터 (bloom filter)는 해시 테이블에 비해 공간 효율이 매우 높은 방법이지만,
결정적 솔루션 대신 부정확한 결과를 얻을 수 있다.
블룸 필터는 거짓-부정(flase negative)이 없다는 것은 보장하지만, 거짓-긍정(false positive)은 나올 수 있다.
즉, 특정 우너소가 존재한다는 긍정적인 답변을 받을 경우,
이 원소는 이제 슈뢰딩거의 고양이가 되는 것이다. 있을 수도 있고 없을 수도 있는 것이다.
그러나 특정 원소가 존재하지 않는다는 부정적인 답변을 받았다면 이 원소는 확실히 없는 것이다.
뻐꾸기 해싱과 마찬가지로 블룸 필터도 여러 개의 해시 함수를 사용한다.
보통 두 개의 해시 함수는 충반한 정확도를 기대하기 어렵기 때문에 세 개 이상을 사용해야 한다.
블룸 필터는 실제 값을 저장하지는 않으며,
대신 특정 값이 있는지 없는지 나타내는 부울 타입 배열을 사용한다.
원소를 삽입할 경우, 모든 해시 함수 값을 계산하고 부울 타입 배열에서
이 해시 값에 대응되는 위치의 비트 값을 1로 설정한다.
룩업의 경우, 모든 해시 함수 값을 계산하고
이에 대응되는 위치의 비트 값이 1로 설정되어 있는지를 검사한다.
만약 검사한 모든 비트가 1이면 true를 반환한다.
1이 아닌 비트가 하나라도 있다면 false를 반환하고, 이는 해당 원소가 없음을 의미한다.
그럼 블룸 필터가 왜 결정적이지 않은 것일까?
그 이유는 특정 비트가 다수의 원소에 의해 1로 설정될 수 있기 때문이다.
즉, 특정 값 x와 연관된 모든 비트가 이전에 삽입된 다른 원소 값들에 의해
모두 1로 설정되어 있을 가능성이 있다는 뜻이다.
이러한 경우 x에 대한 룩업 함수는 true를 반환할 것이다.
이처럼 특정 원소가 있다고 잘못 판단하는 것을 거짓-긍정이라고 한다.
원소 개수가 많아질수록 거짓-긍정이 발생할 가능성은 증가한다.
그러나 x와 연관된 비트 중 하나라도 1로 설정되어 있지 않다면 x가 확실하게 없다고 말할 수 있다.
그러므로 거짓-부정은 발생할 수 없다.
부울 배열의 모든 원소가 true 또는 1로 설정될 경우, 이 배열은 포화 상태가 된다.
이 상태에서 룩업 함수는 항상 true를 반환하고,
삽입 함수는 블룸 필터 상태에 아무런 영향을 주지 못한다.
'컴퓨터 프로그래밍 공부 > 자료구조와 알고리즘' 카테고리의 다른 글
| 열혈 자료구조 - 재귀적 호출의 이해 (1) | 2024.01.29 |
|---|---|
| 열혈 자료구조 - 알고리즘 성능 분석 (0) | 2024.01.29 |
| 해시 테이블과 블룸 필터 (1) - 해시 테이블이란 (2) | 2024.01.05 |
| 트리 - 상하 반전된 형태 (0) | 2023.12.29 |
| 컨테이너 어뎁터, std::stack, std::queue, std::priority_queue (0) | 2023.12.11 |