힙을 이용한 중앙값 구하기
중앙값 먼저 해보자
이번 게시글에서는
머신 러닝, 데이터 분석 응용 프로그램에서 접할 수 있는 문제를 풀어보고자 한다.
어떤 소스로부터 한 번에 하나의 데이터를 연속적으로 받는다고 가정하자.
그리고 매번 데이터를 받을 때마다
지금까지 받은 데이터의 중앙값을 계산한다고 가정하겠다.
간단한 방법은 매번 데이터를 받을 때마다 모든 데이터를 정렬하고,
그 중에서 가운데 원소를 반환하는 것이다.
그러나 이러한 작업은 정렬 연산 때문에 O(N log N)의 시간 복잡도를 가진다.
들어오는 데이터양이 늘어날수록 이 방식은 매우 많은 리소스를 사용하게 된다.
여기서는 힙을 이용해서 최적화하는 방법을 알아보자!
1. 먼저 필요한 헤더 파일을 포함하고
두 개의 힙을 사용해서 데이터를 저장할 것이다.
하나는 최대힙, 하나는 최소힙이다.
새로 들어오는 데이터가 기존 데이터의 중앙값보다 작으면 최대 힙에 저장하고,
새로 들어오면 데이터가 기존 데이터의 중앙값보다 크면 최소 힙에 저장하는 것이다.
이런 방식을 사용하면 두 힙의 최상단 원소를 이용해서 중앙값을 계산할 수 있다.
#pragma once
#include <iostream>
#include <queue>
#include <vector>
class median
{
public:
std::priority_queue<int> maxHeap;
std::priority_queue<int, std::vector<int>, std::greater<int>> minHeap;
- maxHeap: 중앙값 이하의 값들을 관리하고, 그 중에서 가장 큰 값을 최상단에 유지
- minHeap: 중앙값보다 큰 값들을 관리하고, 그 중에서 가장 작은 값을 최상단에 유지
왜 maxHeap과 minHeap이 필요한가?
- 중앙값을 효율적으로 찾기 위해:
- 홀수 개의 값이 입력된 경우: maxHeap과 minHeap의 크기가 다르므로,
크기가 더 큰 힙의 최상단 값이 중앙값이 된다. - 짝수 개의 값이 입력된 경우: maxHeap과 minHeap의 최상단 값을
평균 내어 중앙값을 구할 수 있다.
- 홀수 개의 값이 입력된 경우: maxHeap과 minHeap의 크기가 다르므로,
- 힙을 통한 중앙값 유지:
- maxHeap과 minHeap을 사용하면,
새 값을 삽입할 때마다 O(log n)의 시간 복잡도로 힙의 균형을 유지할 수 있다.
따라서, 중앙값을 빠르게 계산할 수 있는 것이다.
- maxHeap과 minHeap을 사용하면,
2. 새로 들어온 데이터를 저장하는 insert() 함수를 작성하자.
void insert(int data) {
if (maxHeap.size() == 0) {
maxHeap.push(data);
return;
}
if (maxHeap.size() == minHeap.size()) {
if (data <= get())
maxHeap.push(data);
else
minHeap.push(data);
return;
}
if (maxHeap.size() < minHeap.size()) {
if (data > get()) {
maxHeap.push(minHeap.top());
minHeap.pop();
minHeap.push(data);
}
else
maxHeap.push(data);
return;
}
if (data < get()) {
maxHeap.push(maxHeap.top());
maxHeap.pop();
maxHeap.push(data);
}
else
minHeap.push(data);
}
3. 저장된 원소로부터 중앙값을 구하여 반환하는 get() 함수를 작성해보자.
double get()
{
if (maxHeap.size() == minHeap.size())
return (maxHeap.top() + minHeap.top()) / 2.0;
if (maxHeap.size() < minHeap.size())
return minHeap.top();
return maxHeap.top();
}
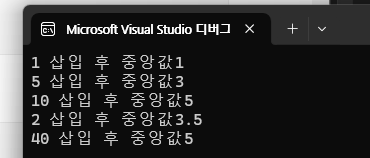
실행 결과
// 중앙값을 찾기 위한 클래스
class median {
public:
// 큰 값을 저장하는 최대 힙 (기본적으로 내림차순)
std::priority_queue<int> maxHeap;
// 작은 값을 저장하는 최소 힙 (std::greater를 사용하여 오름차순으로 저장)
std::priority_queue<int, std::vector<int>, std::greater<int>> minHeap;
// 새로운 데이터 삽입 함수
void insert(int data) {
// maxHeap이 비어 있으면 데이터를 maxHeap에 넣고 종료
if (maxHeap.size() == 0) {
maxHeap.push(data);
return;
}
// maxHeap과 minHeap의 크기가 같을 때
if (maxHeap.size() == minHeap.size()) {
if (data <= get()) // 삽입할 데이터가 현재 중앙값 이하라면 maxHeap에 추가
maxHeap.push(data);
else // 중앙값보다 크면 minHeap에 추가
minHeap.push(data);
return;
}
// minHeap의 크기가 더 클 때
if (maxHeap.size() < minHeap.size()) {
if (data > get()) { // 삽입할 데이터가 현재 중앙값보다 크다면
maxHeap.push(minHeap.top()); // minHeap에서 최솟값을 maxHeap으로 이동
minHeap.pop();
minHeap.push(data); // 새 데이터를 minHeap에 추가
} else {
maxHeap.push(data); // 중앙값보다 작다면 maxHeap에 추가
}
return;
}
// maxHeap의 크기가 더 클 때
if (data < get()) { // 삽입할 데이터가 현재 중앙값보다 작다면
minHeap.push(maxHeap.top()); // maxHeap에서 최댓값을 minHeap으로 이동
maxHeap.pop();
maxHeap.push(data); // 새 데이터를 maxHeap에 추가
} else {
minHeap.push(data); // 중앙값보다 크면 minHeap에 추가
}
}
// 중앙값을 반환하는 함수
double get() {
// 두 힙의 크기가 같으면 중앙값은 두 힙의 최상단 값의 평균
if (maxHeap.size() == minHeap.size())
return (maxHeap.top() + minHeap.top()) / 2.0;
// minHeap이 더 크면 중앙값은 minHeap의 최상단 값
if (maxHeap.size() < minHeap.size())
return minHeap.top();
// maxHeap이 더 크면 중앙값은 maxHeap의 최상단 값
return maxHeap.top();
}
};'컴퓨터 프로그래밍 공부 > 자료구조와 알고리즘' 카테고리의 다른 글
| 자기 전 누워서 정리하는 배열과 리스트 (0) | 2024.11.27 |
|---|---|
| 힙을 이용한 데이터 리스트 병합 (0) | 2024.11.18 |
| 힙 (0) | 2024.10.31 |
| 트리를 이용한 파일 시스템 자료 구조 만들기 (1) | 2024.10.29 |
| 해쉬 테이블 - Collison 문제 해결책 (1) | 2024.10.15 |