행렬이란?
행렬이란 영어로 'matrix'라고도 하며, 수 또는 다항식 등을 직사각형 모양으로 배열한 것이다.
영단어 'matrix' 의 사전적 의미중 가장 첫 번째 뜻은
(숫자, 기호 등을 가로, 세로로 나열해 놓은) 행렬[매트릭스]
라고 정의되어 있다.
즉, 수, 문자, 함수 등을 네모꼴 괄호 안에 배치하여 놓은 것이다.
- 각각의 수 또는 함수 등을 원소/ 성분/ 요소 (element, component)로 갖는다.
행렬의 용도
행렬의 용는 크게 두 가지로 나뉜다.
- 정적인 사용
- 정보를 표로써 정형화시켜, 저장하고 처리하는데 사용된다. ( ex) 엑셀 프로그램 등 )
- 연립 선형 방정식의 표기를 간소화시킨다.
- 시각적 이미지 및 디지털 음을 전송하는 수학적 처리에 사용된다.
- 동적인 사용
- 선형 대수 방정식, 선형 미분방정식, 비선형 미분방정식의 풀이 및 해의 분석의 기초가 된다.
수 많은 미지수를 갖는 선형 연립방정식을 테이블 형식을 이용, 해를 구하는 수학적 도구이다.
.. 연립 선형 방정식을 동시에 만족시키는 근(해)을 구할 때 유용하다.
※ 특히, 수학적 공간 간의 변환/매핑에 활용 된다.
- 백터를 다른 벡터로 변환/변형/적용시키는 어떤 함수로서의 역할을 갖는 행렬
즉, 행렬은 선형성이라는 성질을 갖는 특수한 함수이다.
plus 개념 열기++
선형성이란?
선형성 도는 선형은 직선처럼 똑바른 도형,
또는 그와 비슷한 성질을 갖는 대상이란 뜻으로
이러한 성질을 갖고 있는 변환 등에 대하여 쓰는 용어이다.
plus 개념 닫기++
다음과 같은 예시가 행렬에 대한 예시이다.

이 예시의 행렬은 실수 1, 9, -13, 20, 5, -16을 2 x 3 직사각형 위에 배열한 행렬은 다음과 같다.
행렬에는 덧셈과 스칼라배, 곱셈 연산이 존재한다.
크기가 같은 두 행렬은 같은 위치의 성분별로 더할 수 있으며,
첫째 행렬의 열과 둘째 행렬의 행의 수가 같은 두 행렬은 첫째 행렬의 각 행벡터와
둘째 행렬의 각 열벡터의 스칼라곱을 통해 곱할 수 있다.
곱셈의 교환 법칙이나 소거 법칙 등 복소수의 일부 성질들은
행렬 연산에서 더 이상 성립하지 않는다.

행렬의 표기는 다음과 같은 이미지이다.

위와 같이 행렬의 표기는 대문자 A,B,C 또는 A,B,C 등이며
표기 형식은 크기 ( m x n ) 를 갖는 행렬 A는 위와 같이 표기한다.
이처럼 소문자로 표현하면 보통 임의의 A행렬의 a성분 i행 j열에 있는 성분을
다음과 같이 표기한다
aij
행렬 내 특정 행,열 표기

행수 및 열수가 같은 (n x n) 행렬을 정방행렬이라 하고,
이때 n을 차수(order)라 한다.
원소 a11, a22, a33 . . . . . ann 을 포함하는 대각선을 '주 대각선 (principal diagonal)'이라고 한다.
행렬로써의 백터는
1개의 행 또는 열 만의 행렬을 말한다.
- 1개의 행 또는 열 만의 행렬을 말하며

게임 수학에서 벡터를 구하는 x y z 는 보통 열 벡터를 사용한다.
단위행렬
왼쪽 위에서 오른쪽 아래로 대각선 방향 (↘)의 성분이 1이고 다른 성분은
모두 0인 n차 정사각행렬을 n차 단위행렬이라고 하고 기호로는 E로 나타낸다.
(1) E(n차 단위행렬) : AE = EA = A (A: n차 정사각행렬)
(2) E의 특징
- 행렬의 곱셈에 대한 항등원
- (i,i)의 성분이 모두 1이고, 그 밖의 성분이 모두 0인 정사각행렬
ex)
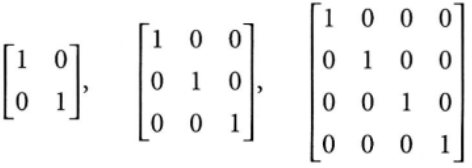
여기서 1이 2로 바뀌면
이러한 행렬은 다음과 같이 표기하여 쓸 수 있다.
2 곱하기 단위행렬인 2E로 표기할 수 있다.
그러면 1자리에 k가 오면
kE로 표기할 수 있다. (단, k가 0이 아닐 때)
스칼라로 치면 단위행렬은 1에 대응한다.
영행렬
선형대 수학에서 영행렬은 모든 성분이 0인 행렬이다.
행렬의 덧셈의 항등원을 이룬다.
스칼라로 치면 영행렬은 0에 대응한다.
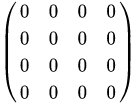
역행렬
A의 역행렬은 곱해서 단위행렬이 나오게 하는 행렬이다.
역행렬을 구하는 방법에는 크게 2가지가 있다.
첫 번째로는, 가우스 조던 소거법과
두 번째로는, 전치행렬, 소행렬, 여인자를 이용하는 방법이다.
이 외에도 공식으로는 라플라스와 크레이머 전개가 있다.
첫 번째 방법인 가우스 조던 소거법은 다음과 같다.
예시로는 2x2 행렬을 들겠다.
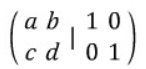
1행에 -(c/a)를 곱하고 2행에 더하면,
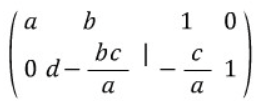
1행을 a로 2행을 d-(bc/a)로 나누면,
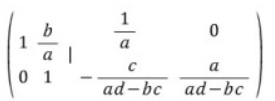
2행에 -(b/a)를 곱한 후 1행에 더하면,
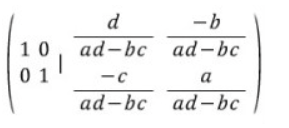
다음과 같은 식이 나온다.
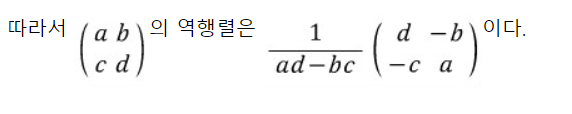
두 번째 방법인 전치행렬, 소행렬, 여인자를 이용한 방법을 응용해 라플라스와 크레이머를
설명하겠다.
게임 개발에서는 3x3, 4x4를 사용하여 크레이머 방식을 선호한다.
일단 라플라스 방법부터 정리해보겠다.
1. 주어진 행렬 (nxn)이 있다. 이를 A라고 두고 A의 전치행렬을 구한다.
(전치행렬이란 i행 j열에 있는 성분을 j행 i열로 바꾼 행렬을 나타낸다.
기호로는 AT (T는 위에 첨자) 라고 나타낸다.)
2. 주어진 행렬의 det를 구한다.
3. 소행렬 Mij를 구한다.
(소행렬 Mij란 AT 행렬에서 i행 j열을 제외한 (n-1)x(n-1)행렬을 말한다.)
4. 여인수 Cij를 구한다.
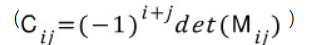
5. 역행렬은 다음과 같다.
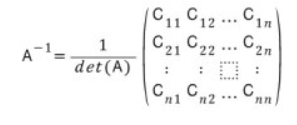
그럼 위의 정보를 기반으로 2x2 행렬을 예시로 대입해보자.
아래는 행렬식이다.
행렬식이란 행렬을 하나의 값으로 만드는 과정이라고 볼 수 있다.
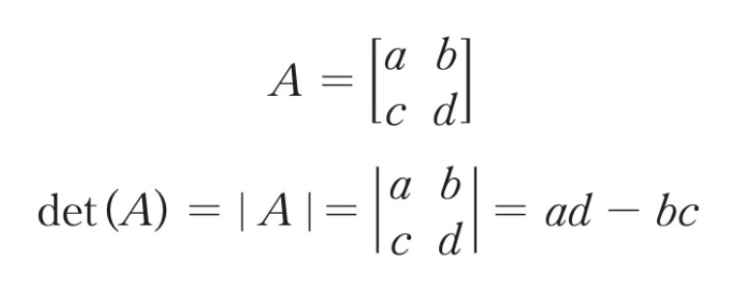
근데 이는 2x2 행렬이니 3x3 행렬을 구하려면 다음과 같이 구해야 한다.
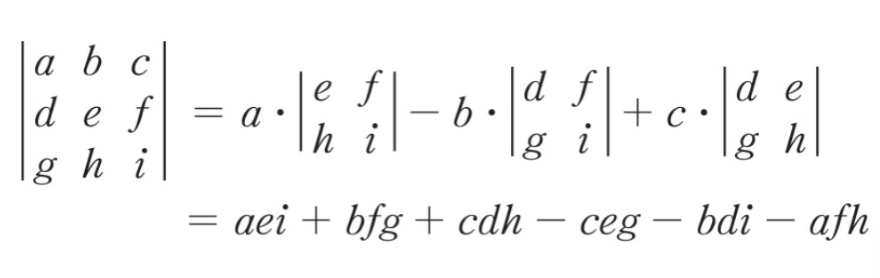
2개로 나누어 값을 구하고,
4차 역시도 2개로 나누어 값을 구한다.
이를 일반화하면 아래와 같은 수식으로 펴현할 수 있다.
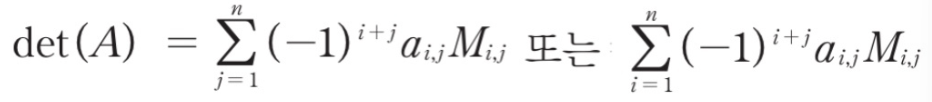
왜 2개가 나오느냐 하면,
행을 기준으로 할 것인지 열을 기준으로 할 것인지가 달라서 3개이다.
라플라스 전개를 여인수 관점에서 풀이하자면서
크레이머 정리로 역행렬을 구한다면,
각각의 행렬 성분에 대응하는 인수들로 행렬 L을 만든다면 다음과 같다.

그 후 원래 행렬과 L의 전치행렬을 곱해준다면,

위과 같은 과정을 정리한다면 아래와 같다.

이러한 크래이머 정리가 왜 라플라스 전개와 연관성이 있냐하면
라플라스 전개와 곱셈의 결과가 같기 때문이다.
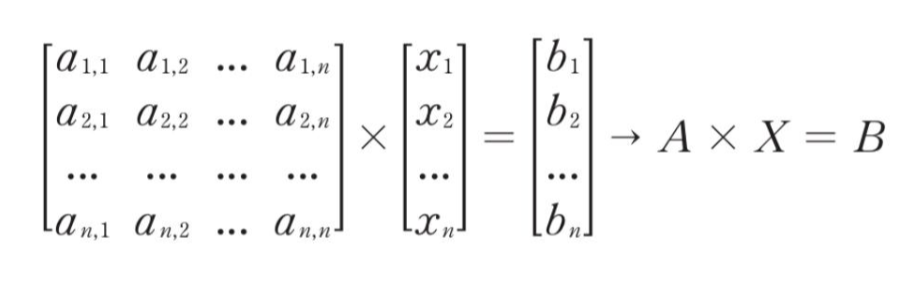
이러한 행렬 곱의 연산, 즉 행렬식을 이용해서 해를 바로 구할 수 있다.
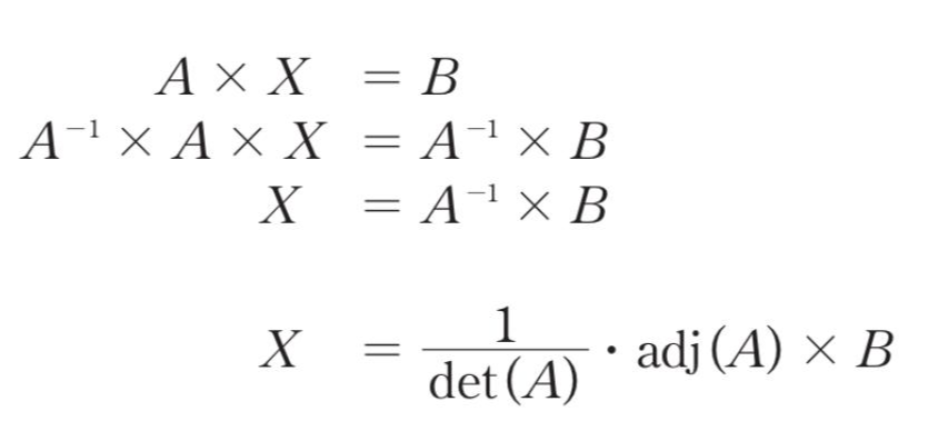
위와 같은 크레이머 정리 식을 사용할 시 0으로 나누는 것은 수학에서 금기되어 있기 때문에
행렬식의 값이 0으로 나오는 것을 주의해야 한다.
역행렬 자료 참고 : https://m.blog.naver.com/jahyone20/220932973637
3x3 역행렬 구하기
역행렬을 구하는 방법에는 크게 2가지가 있다. 1. 가우스 조던 소거법(Gauss-Jordan elimination method)...
blog.naver.com
전치행렬(Transpose Matrix)
전치행렬의 기호는 다음과 같다. AT (T는 위 첨자)
전치를 한다는 것은 행과 열을 서로 맞바꾼 행렬을 전치행렬이라고 한다.
ex)
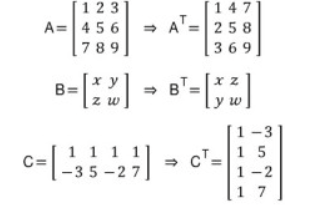
전치 행렬의 성질은 다음과 같다.

행렬의 곱연산
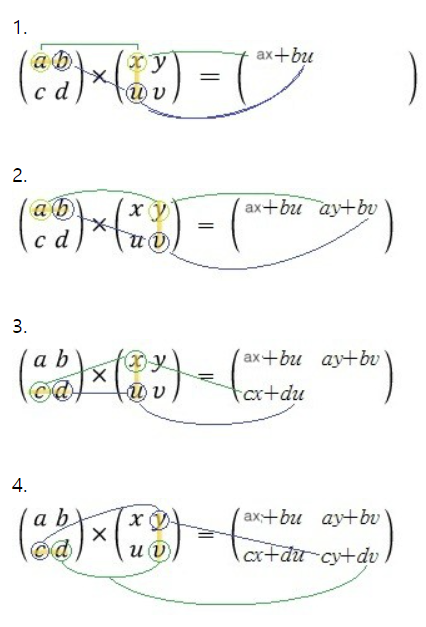
1. 앞 행렬의 1행의 성분 a,b와 뒤 행렬의
1열의 성분 x, u를 같은 위치에 있는 것끼리 곱해준다.
-1 첫번째끼리 즉, a와 x를 곱해서 ax를 얻는다.
-2 두번째끼리 즉, b와 u를 곱해서 bu를 얻는다.
2. 그런 후 결과의 행의 1행의 성분 a,b와 뒤 행렬의 1열의 성분 y, b를
같은 위치에 있는 것끼리 곱해준다.
-1 첫번째끼리 즉, a와 y를 곱해서 ay를 얻는다.
-2 두번째끼리 즉, b와 v를 곱해서 bv를 얻는다.
'컴퓨터 프로그래밍 공부' 카테고리의 다른 글
| CPU와 메모리 (0) | 2023.03.27 |
|---|---|
| 정리 230319 (0) | 2023.03.19 |
| 싱글톤 패턴 + 인스턴스 + 인스턴스화 + 추상화 + 더블 버퍼링 20230227 (0) | 2023.02.28 |
| 호도법, 미리 컴파일 유의 사항 20230224 (0) | 2023.02.24 |
| 삼각함수 (0) | 2023.02.23 |