삽입 정렬(Insertion Sort): 이해와 구현
이번에 소개하는 삽입 정렬은
보는 관점에 따라서 별도의 메모리를 필요로 하지 않는 '개선된 선택 정렬'과 유사하다고 느낄 수 있다.
하지만 전혀 다른 방법으로 정렬을 이뤄나간다.
이와 관련해서 다음 그림을 보자.

위 그림의 배열은 정렬이 완료된 부분과 완료되지 않은 부분으로 나뉘어 있다.
이렇듯 삽입 정렬은 정렬 대상을 두 부분으로 나눠서,
정렬 안 된 부분에 있는 데이터를 정렬 된 부분의 특정 위치에
'삽입'해 가면서 정렬을 진행하는 알고리즘이다.
그럼 다음 그림을 통해서 5,3,2,4,1의 오름차순 정렬 과정을 보이겠다.

위 그림의 가장 윗부분에서 보이듯이,
첫 번쨰 데이터와 두 번째 데이터를 비교하여,
정렬된 상태가 되도록 두 번째 데이터를 옮기면서 정렬은 시작된다.
그리고 이로 인해서 첫 번째 데이터와 두 번쨰 데이터가 정렬이 완료된 영역을 형성하게 된다.
이어서 세 번째, 네 번째 데이터가 정렬이 완료된 영역으로 삽입이 되면서 정렬을 이어 나간다.
물론 정렬된 상태로 삽입하기 위해서는 특정위치를 비워야 하고,
비우기 위해서는 데이터들을 한 칸씩 뒤로 미는 연산을 수행해야 한다.
참고로 구현에 도움이 될만한 말 몇 마디를 하면 다음과 같다.
"정렬이 완료된 영역의 다음에 위치한 데이터가 그 다음 정렬대상이다."
"삽입할 위치를 발견하고 데이터를 한 칸씩 뒤로 밀수도 있지만,
데이터를 한 칸씩 뒤로 밀면서 삽입할 위치를 찾을 수도 있다."
위에서 언급한 '데이터를 한 칸씩 뒤로 밀면서 삽입할 위치를 찾는다'는 것이
의미하는 바를 그림을 통해서 설명하겠다.
이 그림에서는 숫자 3을 정렬이 완료된 영역으로 옮기는 과정을 보이고 있다.

위 그림에서 보이듯이,
삽입위치를 찾는 과정과 삽입을 위한 공간마련의 과정을 구분할 필요가 없다.
어차피 정렬된 영역에서 삽입의 위치를 찾는 것이니,
삽입위치를 찾으면서 삽입을 위한 공간의 마련을 병행할 수 있는 것이다.
그럼 이어서 삽입 정렬의 구현의 예를 보이겠다.
#include <iostream>
#include <vector>
#include <algorithm>
void InserSort(int arr[], int n)
{
int i, j;
int insData;
for (i = 1; i < n; i++)
{
insData = arr[i];
for (j = i - 1; j >= 0; j--)
{
if (arr[j] > insData)
{
arr[j + 1] = arr[j]; // 비교대상 한 칸 밀기
}
else
{
break; // 삽입 위치 찾았으니 탈출!
}
}
arr[j + 1] = insData;
}
}
int main(void)
{
int arr[5] = { 5,3,2,4,1 };
int i;
InserSort(arr, sizeof(arr) / sizeof(int));
for (i = 0; i < 5; i++)
{
printf("%d", arr[i]);
}
printf("\n");
return 0;
}
삽입 정렬(Insertion Sort) : 성능평가
삽입 정렬은 정렬대상의 대부분이 이미 정렬되어 있는 경우 매우 빠르게 동작한다.
그럼 삽입 정렬의 성능평가를 위해서 다음 반복문을 살펴보자.
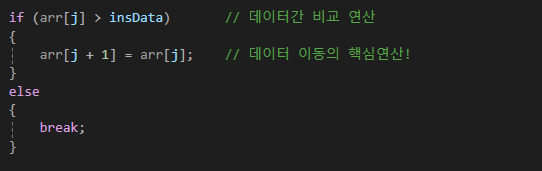
정렬 대상이 완전히 정렬된 상태라면,
안쪽 for문의 if...else문의 조건은 항상 '거짓'이 되어 break문을 실행하게 된다.
따라서 데이터의 이동도 발생하지 않고 if...else문의 조건비교도
바깥쪽 for문의 반복횟수 이상 진행되지 않는다.
하지만 최악의 경우를 고려하면,
이 역시 앞서 보인 두 정렬들과 다를 바 없다.
최악의 경우 안쪽 for문의 if...else문의 조건은 항상 '참'이 되어 break문을 단 한번도 실행하지 않는다.
따라서 바깥쪽 for문의 반복횟수와
안쪽 for문의 반복횟수를 곱한 수만큼 비교연산도, 이동연산도 진행이 되므로,
이를 근거로 비교연산과 이동연산에 대한 빅-오가 다음과 같음을 쉽게 추측할 수 있다.
O(n²)
이러한 추측이 만족스럽지 않다면 다음과 같이 안쪽 for문에 속한
if...else문의 실행횟수에 대한 식을 세워서 정확히 계산을 진행하면 된다.
1 + 2 + 3+ . . . + (n-2) + (n-1)
이 역시 등차수열의 합에 해당한다.
힙 정렬 (Heap Sort) : 이해와 구현
힙 정렬은 힙을 이용한 정렬방식으로 힙의 다음 특성을 활용하여 정렬하는 알고리즘이다.
"힙의 루트 노드에 저장된 값이 가장 커야 한다."
물론 이는 '최대 힙 (max heap)'의 특징이다.
하지만 우리는 다음 특징을 갖도록 힙을 구성할 수도 있다.
"힙의 루트 노드에 저장된 값이 정렬순서상 가장 앞선다."
이러한 힙 정렬의 예제는 다음과 같다.
void HeapSort(int arr[], int n, PriorityComp pc) //힙 정렬 구현 함수
{
. . . .
// 힙 정렬 단계 1: 데이터를 모두 힙에 넣는다
for(i = 0; i < n; i++)
Hinsert(&heap, arr[i]);
// 힙 정렬 단계 2: 힙에서 다시 데이터를 꺼낸다.
for(i = 0; i < n; i++)
arr[i] = HDelete(&heap);
}
보다시피 정렬의 대상인 데이터들을 힙에 넣었다가 꺼내는 것이 전부이다.
그럼에도 불구하고 정렬이 완료되는 이유는, 꺼낼 대 힙의 루트 노드에 저장된 데이터가 반환되기 때문이다.
힙 정렬(Heap Sort) : 성능 평가
언뜻 보면 저장된 데이터를 죄다 힙에 넣었다가
다시 꺼내기 때문에 성능상 이점이 별로 없어 보이지만,
힙 정렬은 지금까지 소개한 정렬들 중 가장 좋은 성능을 가진 알고리즘이다.
비교연산의 횟수를 근거로 하여 힙의 데이터 저장 및 삭제의 시간 복잡도를
다음과 같이 계산한바 있다.
- 힙의 데이터 저장 시간 복잡도 O(log₂n)
- 힙의 데이터 삭제 시간 복잡도 O(log₂n)
따라서 삽입과 삭제를 하나의 연산으로 묶는다면,
이 연산에 대한 시간 복잡도는 다음과 같이 결론 내릴 수 있다.
O(2log₂n)
하지만 숫자 2는 빅-오에서 무시할만한 수준이므로
삽입과 삭제를 하나의 연산으로 묶는다 해도, 이 연산에 대한 시간 복잡도는 여전히 다음과 같다.
O(log₂n)
그럼 정렬과정에 대한 시간 복잡도는 어떻게 될까?
정렬대상의 수가 n개라면, 총 n개의 데이터를 삽입 및 삭제해야 하므로
위의 빅-오에 n을 곱해야 한다.
'컴퓨터 프로그래밍 공부 > 자료구조와 알고리즘' 카테고리의 다른 글
| Stack 구현하기 (0) | 2024.08.02 |
|---|---|
| 완벽한 해싱 & 유니버설 해싱 (0) | 2024.06.15 |
| 동적 계획법의 접근 방식 (1) | 2024.06.09 |
| 우선순위 큐 (0) | 2024.06.06 |
| 동적 계획법 (1) (0) | 2024.05.18 |