
구의 Reflection 수치 값을 변경해주기 전이다.

구 1개만 반사 적용

구 2개에 반사광 적용

바닥까지 반사광 적용
이는 레이트레이싱을 이용한 반사광 적용이다.
반사되는 횟수가 많아질수록 고성능을 요구하기 때문에 컴퓨터 사양에 따라 좀 느려지기도 한다.
해당 이론은 Bilinear Interpolation즉 이중선형 보간과 관련이 있다.
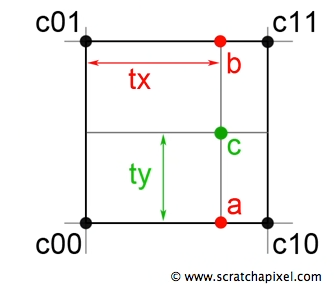
우리는 해당 그림을 통해서 먼저 두개의 선형 보간을 수행하여 a와 b를 계산한 다음
a와 b를 보간하여 c를 찾을 수 있다.
c는 당연히 (tx , ty)의 값을 가지게 될 것이다.
이중선형 보간은 일반 2D 그리드의 임의 위치에 있는 값을 알아야 할 때 사용된다.
이 그리디는 이미지나 텍스처 맵에 사용될 수 있다.
이 예에서는 녹색 점으로 표시된 위치(좌표 cx, cy가 있는 c)에서 값을 찾는 데 이해관계가 있다.
c의 값을 계산하기 위해 먼저 한 방향 (x 방향)으로 두 개의 선형 보간(소개 참조)를 수행하여
b와 a를 얻는다.
그렇게 하기 위해서는 c00 - c10과 c01-c11을 선형적으로 보간하여 tx(여기서 tx = cx)를 사용하여 a와 b를 얻는다.
그런 다음 ty(ty=cy)를 사용하여 c를 얻기 위해 두 번째 방향(y축)를 따라 ab를 선형 보간한다.
x축을 따라 처음 두 값 보간을 시작하든 y축을 따라 보간을 시작하든 상관없다.
이 예에서는 c00-c10과 c01-c11을 보간하여 a와 b를 얻는 것으로 시작한다.
ty를 사용하여 c00-c01과 c10-c11을 보간한 다음 tx를 사용하여 결과 (a 및 b)를 보간할 수도 있다.
코드를 더 쉽게 디버깅하고 작성하려면 축 순서(삼선형 보간의 경우 x,y,z)를 따르는 것이 좋다.
선형 보간법을 수행할 때 일반적으로 t가 1보다 크지 않거나 0보다 작은지
코드에서 확인하고 평가하려는 점이
그리드의 한계를 벗어나지 않는지 확인하는 것이 좋다. 해당 그리드의 해상도는 NxM이다.
(N + 1) x (M + 1) 정점 또는 NxM 정점을 생성해야 하며 그리드의 해상도가 (N-1)x(M-1)이라고 가정해야 한다.
이름에서 알 수 있듯이
쌍선형 보간은 (선 c00 - c10 또는 c00 - c01 또는 c01 - c11)에 있는 경우 함수는 선형이다.
다른 모든 곳에서는 이차적이다.
다음 예시 코드에서는 해당 이미즈의 각 픽셀에 대한 그리드 값(색상)을 보간하여
이미지를 생성하는 코드이다.
많은 이미지 픽셀에는 그리드 좌표와 겹치지 않는 좌표가 있다.
우리는 이러한 "픽셀" 위치에서 보간된 색상을 계산하기 위해 쌍선형 보간을 사용한다.
void testBilinearInterpolation()
{
// testing bilinear interpolation
int imageWidth = 512;
int gridSizeX = 9, gridSizeY = 9;
Vec3f* grid2d = new Vec3f[(gridSizeX + 1) * (gridSizeY + 1)]; // lattices
// fill the grid with random colors
for (int j = 0, k = 0; j <= gridSizeY; ++j)
{
for (int i = 0; i <= gridSizeY; ++i, ++k)
{
grid2d[j * (gridSizeX + 1) + i] = Vec3(drand48(), drand48(), drand48());
}
}
//now computer our final image3 using bilinear interpolation
Vec3f* imageData = new Vec3[imageWidth * imageWidth], * pixel = imageData;
for (int j = 0; j < imageWidth; ++j)
{
for (int i = 0; i < imageWidth; ++i)
{
// convert i, j to grid coordinates
T gx = i / float(imageWidth) * gridSizeX; // Be Careful to interpolate bounderi
T gy = j / float(imageWidth) * gridSizeY; // Be Careful to interpolate bounderi
int axi = int(gx);
int gyi = int(gy);
const Vec3f& c00 = grid2d[gyi * (gridSizeX + 1) + gxi];
const Vec3f& c10 = grid2d[gyi * (gridSizeX + 1) + (gxi + 1)];
const Vec3f& c01 = grid2d[(gyi + 1) * (gridSizeX + 1) + gxi];
const Vec3f& c11 = grid2d[(gyi + 1) * (gridSizeX + 1) + (gxi + 1)];
*(pixel++) = bilinear(gx - gxi, gy - gyi, c00, c10, c01, c11);
}
}
saveToPPM("./bilinear.ppm", imageData, imageWidth, imageWidth);
delete[] imageData;
}


이중선형 함수는 템플릿으로 만들어졌다면,
모든 유형 (플로트, 색상 등)의 데이터를 보간할 수 있다.
첫 번째 방법(xx행에서 xx행)이 더 읽기 쉽지만,
보간이 4개의 꼭지점(c00, c01, c10 및 c11에는 일부 계수가 곱해집니다.
예를 들어 (1 - tx) * (1 - ty)c00에 대한 가중치 계수입니다.
쌍선형 보간법의 장점은 구현이 빠르고 간단하다는 것이 특징이다.
이중선형 보간이 보간 결과를 사용하려면 목적에
따라 반드시 허용되지 않는 일부 패턴을 생성한다는 것을 알 수 있다.
더 나은 결과가 피요한 경우 2차 이상의 보간 기능과 관련된 고급 보간 기술을 사용해야 한다.
출저 : https://www.scratchapixel.com/lessons/mathematics-physics-for-computer-graphics/interpolation/bilinear-filtering.html
'그래픽스 > DX11' 카테고리의 다른 글
| DX11 - 무게중심좌표계 이론 (0) | 2024.09.24 |
|---|---|
| D3D11 - 벡터와 레스터화 (1) | 2024.09.13 |
| DX11 - 수퍼 샘플링 (0) | 2024.04.17 |
| DX11 - 텍스춰링 (1) | 2024.04.03 |
| DX11 보간 (1) | 2024.03.27 |